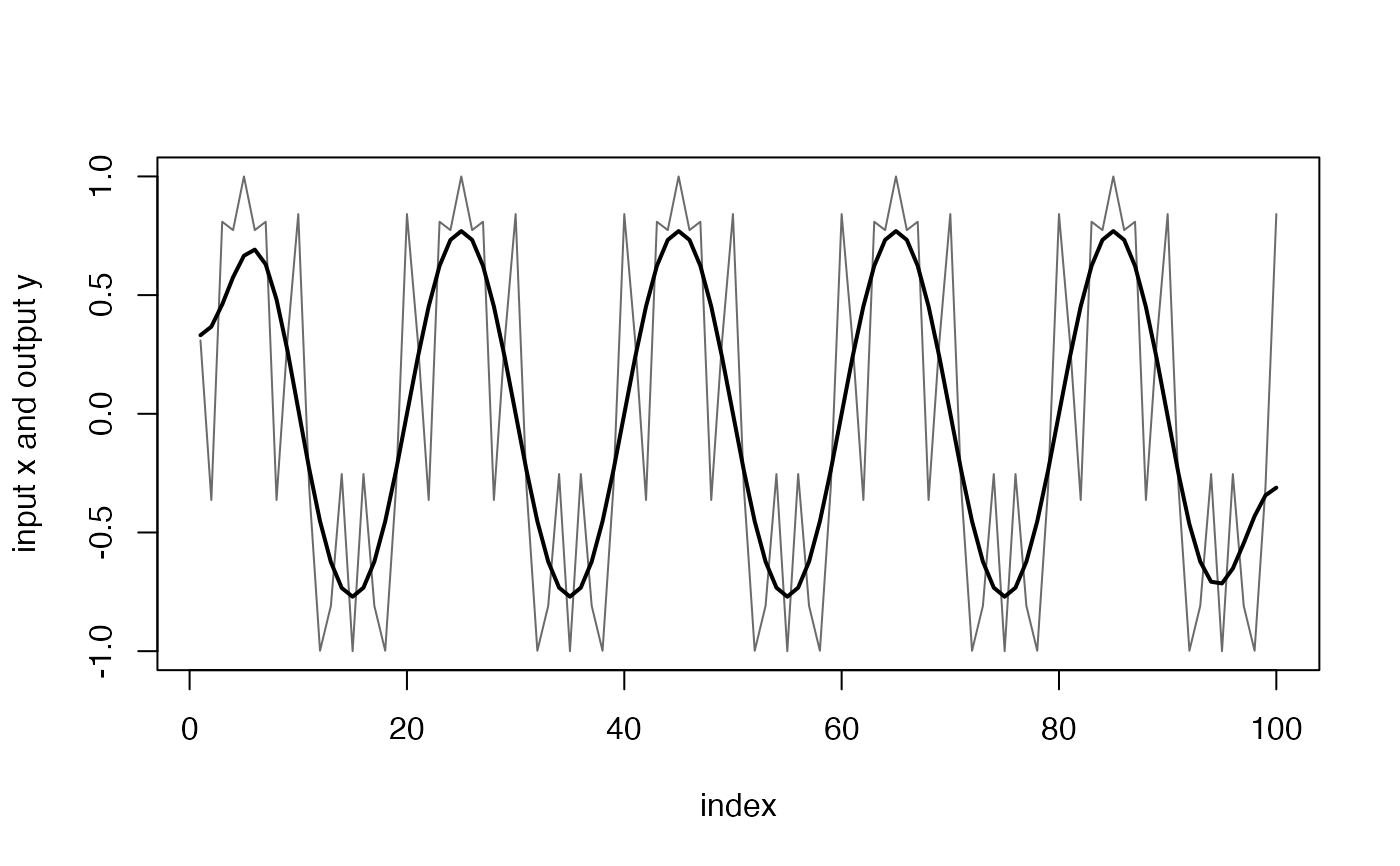
This function is used to specify or carry out delay-free filtering using a linear-phase (symmetric) FIR filter followed by group delay correction. Delay-free filtering is needed when the relative timing between signals is important e.g., when integrating signals that have been sampled at different rates.
Arguments
- x
The signal to be filtered. It can be multi-channel with a signal in each column, e.g., an acceleration matrix. The number of samples (i.e., the number of rows in x) must be larger than the filter length, n.
- n
The length of symmetric FIR filter to use in units of input samples (i.e., samples of x). The length should be at least 4/fc. A longer filter gives a steeper cut-off.
- fc
The filter cut-off frequency relative to sampling_rate/2=1. If a single number is given, the filter is a low-pass or high-pass. If fc is a vector with two numbers, the filter is a bandpass filter with lower and upper cut-off frequencies given by fc(1) and fc(2). For a bandpass filter, n should be at least 4/fc(1) or 4/diff(fc) whichever is larger.
- qual
An optional qualifier determining if the filter is: "low" for low-pass (the default value if fc has a single number), or "high" for high-pass. Default is "low".
- return_coefs
Logical. Return filter coefficients instead of filtered signal? If TRUE, the function will return the FIR filter coefficients instead of the filtered signal. Default is FALSE.
Value
If return_coefs is FALSE (the default), fir_nodelay() returns the filtered signal (same size as x). If return_coefs is TRUE, returns the vector of filter coefficients only.
Note
The filter is generated by a call to fir1: h <- fir1(n, fc, qual).
h is always an odd length filter even if n is even. This is needed to ensure that the filter is both symmetric and has a group delay which is an integer number of samples.
The filter has a support of n samples, i.e., it uses n samples from x to compute each sample in y.
The input samples used are those from n/2 samples before to n/2 samples after the sample number being computed. This means that samples at the start and end of the output vector y need input samples before the start of x and after the end of x. These are faked by reversing the first n/2 samples of x and concatenating them to the start of x. The same trick is used at the end of x. As a result, the first and last n/2 samples in y are untrustworthy. This initial condition problem is true for any filter but the FIR filter used here makes it easy to identify precisely which samples are unreliable.
This function is based on the Matlab fir_nodelay() function in the matlab animaltags tool kit, and currently uses fir1() from package gsignal. Whether we use fir1 from the signal or the gsignal R package, the filter coefficients returned are *not* exactly identical to the ones returned by Matlab's fir1() function and we don't have a simple remedy for this.